Why are these new shadow map techniques filterable!?

I’ve only been doing graphics stuff seriously for about a year.  One of the first things I tackled was shadow mapping.  I got a simple shadow map implementation going and then implemented Variance Shadow Maps.  It’s based on statistics and the big deal is that you can filter your shadow map and get filtered shadows as a result.  At the time, I didn’t understand why that was true. I had assumed it was a special property of the Chebychev Inequality.  I just implemented it and went on.  Yesterday, I quickly tested Exponential Shadow Maps.  While looking at it, it finally struck me why it was filterable:

These new shadow map techniques are smooth functions based on the occluder and receiver distances to the light!

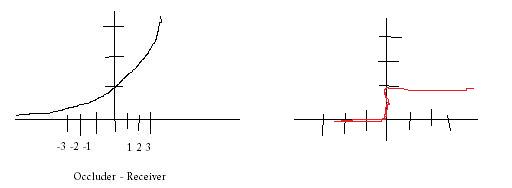
Above is my Microsoft Paint created graphs (grabbed this style of graphing from Pat Wilson heh). On the left is ESM, you can see that it smoothly drops from 1 (fully lit) to 0 (fully shadowed). So if you massage your shadowmap and you get values on the x-axis (which is occluder - receiver), you’ll see that there will be a border of grey values (basically from -5 to 0 in the graph above, btw this is not what e^(c*o-r) actually looks like, heh). On the right, standard shadow mapping is just a step function. If you move this a little bit below zero, you’re immediately shadowed completely.

This is a also a reason why you don’t need to worry about shadow map bias as much with these new techniques. Because the shadow function isn’t all or nothing, if occluder - receiver is -.9999, you’re going to look basically lit. But in standard shadow mapping, -.9999 is fully shadowed, and you’ll get shadow acne.

So you could draw any random function as a 1d texture and use that for shadow mapping!  These other techniques are just ways of creating that function in a way that is fast and makes sense visually.

The silly thing is that I knew why standard shadow maps were not filterable from the get-go, I just didn’t “invert” my thinking to figure out why these new methods were filterable.