Graphics
Torque 3D Lighting System Video
Just a quick link post today. Here’s a video of the lighting system I’ve worked on with Pat Wilson and Tom Spilman. I’m mostly responsible for the dark pixels in the video. ;)
Also, I got a new personal best score at Robotron today: 624k. I’m slowly inching up to a million.
Probabalistic Shadow Map Technique Comparisions
This is a quick slideshow of screenshots and notes about various shadow map techniques. I hope to continue adding to this in the future. The notes are pretty terse and probably not useful unless you read the source papers. ;)
Math Debugging
I’ve gotten a late start on this rendering thing. One of the pieces I’ve been struggling with is math. I’ve improved quite a bit over the past year and I’m actively educating myself to catch up. Recently, a friend of mine asked me for some help with a matrix problem. Here’s what I told him to help him debug (I wish I could go back in time and tell myself this!):
- If you’ve got a series of matrix multiplications, make all of the terms identity. Then change each to be a real value one by one. For example: Let’s say you’re rendering an object with a lot of sub-meshes or sub-objects. You’d set the subobject’s transforms to identity and the main object’s transform to identity. This will make everything render on top of each other. From here, you concentrate on getting the sub-objects transforms correct, then finally work on the main object’s transform.
- Try creating situations where the results of an equation would be identity. For example: When using a shadow map, you need a matrix which transforms a point from camera space to light space. If the camera and the light have the same transform (and FOV, view distance, etc) then this matrix will be identity. If you run it through your code and it’s not, you know you’ve got some problems to solve!
- Pay close attention to what space your source data is in. If you feed object space points to a function that expects world space points, it’s not going to work!
- Check out Octave, it’s basically a free version of MATLAB. You can use this to play with matrices and vectors, probably much quicker than you can do in-engine.
These are just general divide and conquer debugging tips applied to math. But for a person new to large amounts of math in programming, it can be non-obvious to think about applying those debugging techniques to math problems. Does anyone out there have their own favorite math debugging tips?
Quick PIX trick
Let’s say you’ve got a render state problem. If object A is on the screen at the same time object B is on the screen, object A gets screwed up. Here’s a quick way of using PIX to track it down:
- Take a snapshot of the frame that works and a snapshot of the frame that fails.
- In PIX, find the draw call that draws object A in the frame that works
- Go to the device state tab
- Copy and paste each page of state into a text file
- Repeat for the frame that fails, save this to a separate text file.
- Diff the text files with your favorite diff tool!
This is much easier than trying to diff the states manually within PIX itself. PIX should have a draw call diff as part of its standard functionalty!
Why are these new shadow map techniques filterable!?
I’ve only been doing graphics stuff seriously for about a year. One of the first things I tackled was shadow mapping. I got a simple shadow map implementation going and then implemented Variance Shadow Maps. It’s based on statistics and the big deal is that you can filter your shadow map and get filtered shadows as a result. At the time, I didn’t understand why that was true. I had assumed it was a special property of the Chebychev Inequality. I just implemented it and went on. Yesterday, I quickly tested Exponential Shadow Maps. While looking at it, it finally struck me why it was filterable:
These new shadow map techniques are smooth functions based on the occluder and receiver distances to the light!
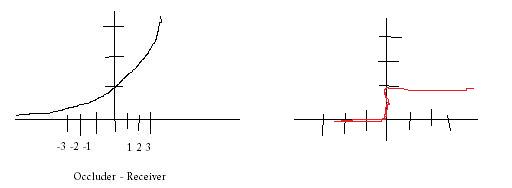
Above is my Microsoft Paint created graphs (grabbed this style of graphing from Pat Wilson heh). On the left is ESM, you can see that it smoothly drops from 1 (fully lit) to 0 (fully shadowed). So if you massage your shadowmap and you get values on the x-axis (which is occluder - receiver), you’ll see that there will be a border of grey values (basically from -5 to 0 in the graph above, btw this is not what e^(c*o-r) actually looks like, heh). On the right, standard shadow mapping is just a step function. If you move this a little bit below zero, you’re immediately shadowed completely.
This is a also a reason why you don’t need to worry about shadow map bias as much with these new techniques. Because the shadow function isn’t all or nothing, if occluder - receiver is -.9999, you’re going to look basically lit. But in standard shadow mapping, -.9999 is fully shadowed, and you’ll get shadow acne.
So you could draw any random function as a 1d texture and use that for shadow mapping! These other techniques are just ways of creating that function in a way that is fast and makes sense visually.
The silly thing is that I knew why standard shadow maps were not filterable from the get-go, I just didn’t “invert” my thinking to figure out why these new methods were filterable.
Random notes on Quadric Error Metrics
Mesh decimation is the process of simplifying a mesh. Most of the time you do this to improve performance. A popular method of mesh decimation is called the edge collapse. You move a vertex from one side of an edge in a mesh to the other. Then you delete any degenerate triangles. One of the first things you need to do is decide which edge is the best to collapse! Computing a Quadric Error Metric) (QEM) for a vertex is a method of determining the cost of an edge collapse.
The basic idea is that the QEM gives you the sum of the squared distance of a point to a set of planes. Then for each point in your mesh, you build a set of planes from the triangles it belongs to and you can use the QEM to compute the cost for moving a vertex from its starting position to a new position. It has some neat properties. If you add two quadrics together, it’ll return the same results as if you built a quadric with all of their source planes from scratch. This is convenient during mesh decimation because you can combine quadrics after performing an edge collapse.
After implementing the QEM code, I noticed some things:
-
If you calculate the error for a vertex without moving it, it should be zero. This is one way to validate your implementation of QEM.
-
If you look at the formulas given in section 5.1 of (http://graphics.cs.uiuc.edu/~garland/papers/quadric2.pdf). You’ll see that it calculates two edge vectors to define a plane. The vectors are defined (in pseudo code) as: e1 = q-pe1.normalize()side2 = r - p
side2.normalize() // <- This is not in the original paper
e2 = side2 - (e1 dot (side2)) * e1
e2.normalize()It turns out that it’s better to normalize side2 before calculating e2. You can confirm this by doing a dot product between e1 and e2, it should be very close to zero. For larger triangles, or nearly degenerate triangles, I ended up with e1 & e2 not being perpendicular at all. This just causes havok later on, producing large negative values for the distance calculation, which should be impossible! ;)
-
The verts that you choose for p,q,r matter. If you play with the ordering, you can see that the error will change a bit. I tried to make sure that (q-r) dot (r - p) was as close to zero (as close to perpendicular) as possible. So I swap p,q,r until I find the combination that’s closest to zero.
-
For some inputs, it works much better with doubles vs. floats. But even with doubles, you must make sure that the double precision rounding is enabled. DirectX will often change this on you unless you tell it not too! If I had remembered this sooner (this has caused other problems for coworkers), I probably would not have figured out 1 & 2 above! ;)
I’m working on improving the rest of the decimation system. Some of that work will involve not feeding the QEM bad triangles that are nearly degenerate which will make the changes above less important. But now that I’ve explored and fixed some of these issues I’m confident that this brick in the decimation system is solid!
A PIX debugging session
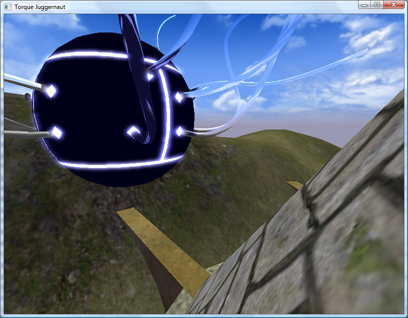
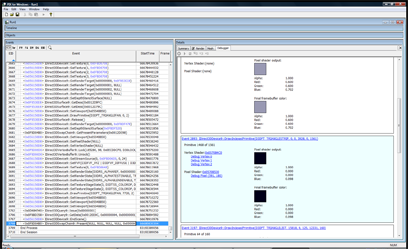
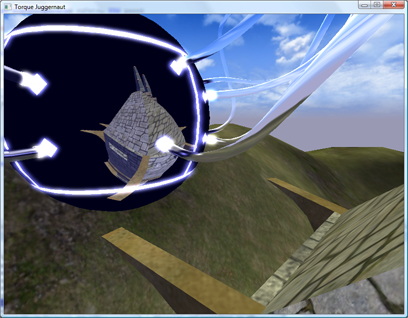
Here’s an article I’ve been meaning to write for a little while. It’s about PIX, the DirectX utility that ships with the DirectX SDK. It’s a great utility for tracking down rendering issues. The point of this article isn’t really to explain it in great detail, because it’s easy to use. It’s mostly to expose people to the tool and encourage you to check it out! This is a debugging session I did after tracking down a crash bug in dynamic cubemaps in the upcoming TGEA release. The crash bug was pretty easy to find. But when I fixed it, I got this result:
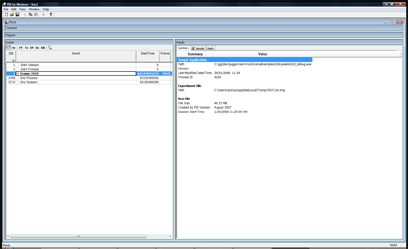
The “spider ball” in this image should be reflecting the tower it is next to, what gives? Let’s use PIX to figure it out. First, to launch PIX, find it under DirectX Utilities under the DX SDK folder. You’ll get a blank screen. Next, select File->New Experiment. Then for “Program Path”, enter the path to your executable. Then, select the “A single-frame capture to Direct3D whenever F12 is pressed.” radio button. Finally, hit the “Start Experiment”. This will launch the app. The next step is to get your app to render your bug. In this example, I moved the camera so I was looking at the spider ball again and hit the F12 key. The game will pause while PIX records all of the DirectX API calls and state into a log file. Then quit. You’ll end up with a screen like this:
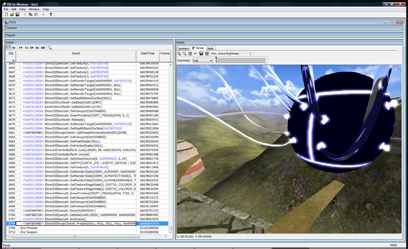
The treeview in the lower left pane is a list of all DirectX calls made during the frame that was recorded. If you click on the render tab in the right pane PIX will show you the scene up to the API call selected in the left pane. You can learn a lot about how an app renders by just hitting the “D down” button and watching the scene draw step by step in the render pane.
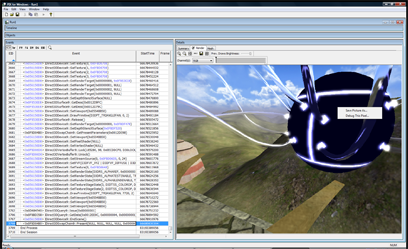
It’s cool to have all of this information at our fingertips, but it’d be cooler if we could filter it down to what we’re interested in. By right-clicking on a pixel in the scene and selecting “Debug This Pixel” we can do just that.
This will replace the render view with a list of all of the API calls that changed the color of that pixel. It’s a life story of that pixel for that frame. You can click on each of the links displayed to move the current selection in the treeview in the left hand pane to that API call.
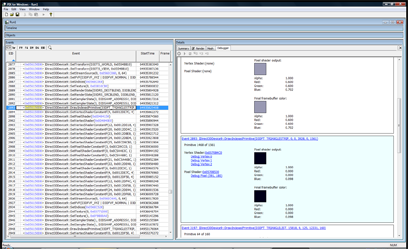
In this next image, I just picked the first pixel that was black, which should get me to the API call I feel is generating the wrong image. It’s event 2893.
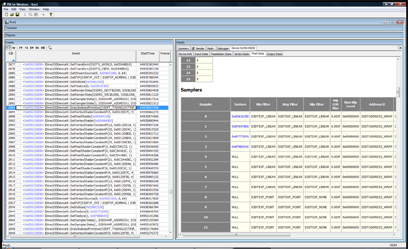
Now we can examine the state of D3D at the time of this call. This is awesome stuff! Rendering with DirectX (and OpenGL) basically involves setting up a large state machine. The types of states are rendering states, textures, texture sampling states, shaders, shader constants, and the list goes on. If any one of these states is incorrect, you’ll get rendering bugs. They can be hard to track down without a tool which allows one to examine the state of D3D. Often we have to do ad-hoc state checks by dumping textures to disk or querying the device and logging the state info out to a file. PIX provides the ability to check state without modifying your code. Getting back to my dynamic cubemap problem, the first question we must answer is: Is the dynamic cubemaptexture being rendered correctly? If it is being generated correctly, are we actually using it during the draw call? Let’s find out! Double click on the blue hexadecimal address to the left of the API call in the treeview in the left hand pane. In this example, it’s 0x056150D8. This will change the right hand pane to a view of the device. We can see a lot of state here. I want to look at the textures, so I choose “Pixel State” from the tabs and scroll down to the “Sampler” section. This section allows one to look at all of the current textures that are active during a draw call. Many bugs are just due to the wrong texture being bound, or no texture is bound at all!
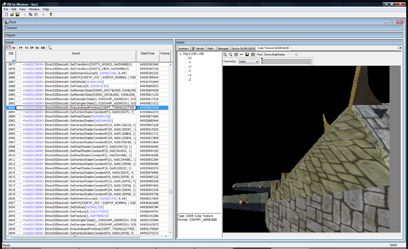
To actually look at the texture, just double click on the blue hexadecimal address in the “texture” column. In the next picture, you can see the cubemap texture has data in it! This is good news, that means I can ignore all of the code that deals with generating the cubemap.
Next, I wanted to look at the pixel shader code that is used. Mostly because I forgot how the cubemap was working at the time. I wanted to see what other dependencies it might have: other textures, shader constants, etc. To do this, go back to the debugger frame that showed the history of the pixel and click on “Debug pixel (xx,xx)”. This will bring up the pixel shader that was used.
Looking at the shader, it only samples the cubemap and doesn’t rely on any shader constants. It’s time to look at the vertex shader to see what it passes to the pixel shader. To do this, just select “Debug Vertex X” in the history view.
Looking at this dump really fast, I could see that it needed to have these vertex shader constants: $modelview @ position 0, $cubeTrans @ position 16, and $cubeEyePos @ position 19. Let’s check the vertex shader constants and see if the data is good. To do this, select “Vertex State” from the tabs and scroll down to the vertex shader constants.
Oh crap! Look at positions 16-19, it’s full of zeros. So the cubemap transform isn’t getting set! I quickly searched the code to see what sets them up and found out that they’ll only be set if the material has “dynamicCubemap” set to true! D’oh! I fixed the material and got the following screen:
That was literally my debugging session, it took about 5 minutes. It could have taken a lot longer if I didn’t have the right tool. Hopefully, this was a good introduction to PIX. There are other uses for it: performance monitoring, resource usage, but this is what I use it for the most. I hope this article makes you reach for PIX the next time you have a rendering bug.
Back to basics: Projection transform
While working on Parallel Split Shadow Maps something that had been tripping me up was calculating the bounding box of a frustum in a light’s clipspace. I need this bounding box in order to scale the projection matrix to look at the piece of the scene that I’m interested in. I’ve noticed that other people have struggled with this problem as well, so I thought I’d post what I found.
My problem: So the problem I’m solving is this: Given a frustum in world space, find the bounding box of that frustum in the light’s clip space. My attack was this:
1. Translate each point of the frustum into light space. 2. Using the light’s projection matrix, translate this point into clipspace. 3. Project the point by dividing by the points .w coordinate. 4. Finally, check against the current min/max points (standard bounding box construction).
Which are the correct general steps. The problem is when a point that was one of the bounding boxes min/max points went behind the light, it wasn’t being counted correctly anymore? What gives?
Quick recap of clipspace/projection:
The clip matrix for D3D looks like this:
| xZoom 0 0 0 | | 0 yZoom 0 0 | | 0 0 (farPlane + nearPlane)/(farPlane - nearPlane) 1 | | 0 0 (nearPlane * farPlane)/(nearPlane - farPlane) 0 |
This basically allows for field of view (xZoom/yZoom) and near/far plane clipping. The goal of the matrix above is to scale x,y,z& w coordinates of a point to the values needed to project it to 2d and to provide clipping information. If 0 <= z <= w, then the point is within the near and far planes. This also works for the x & y coordinates by comparing against -w and w.
For my problem, we can simpify this matrix down to this:
| 1 0 0 0 | | 0 1 0 0 | | 0 0 1 1 | | 0 0 0 0 |
Which turns projection into just dividing x & y by z. This is the way most of us did 3d when we were little kids.
The issue was my mental model of projection was wrong. I basically thought of it as a flattening operation. That is true when the points are all in front of the camera, but when points are behind the camera the x & y coordinates will actually get mirrored due to the z coordinate being negative! So if z = -1 then it’s going to flip x & y, duh!
In my case, I needed to use the absolute value of the w to get the number I needed. I doubt this is an issue that will come up often for people, but I just thought I’d share what I learned by repeating smashing my head against this problem. ;)
Notes: Here’s the slide-deck that triggered this in my head: http://www.terathon.com/gdc07_lengyel.ppt
Slide 7 has a great graphic, basically, the red area is the flipped coordinates.
Example: In front of the camera: untranslated: -10.000000 100.000000 0.000000 1.000000 clipspace: -10.000000 -0.000006 99.909988 100.000000 normalized device coords: -0.100000 -0.000000 0.999100
Behind the camera: untranslated: -10.000000 -100.000000 0.000000 1.000000 clipspace: -10.000000 0.000006 -100.110016 -100.000000 normalized device coords: 0.100000 -0.000000 1.001100
You can see that behind the camera the x&y coordinates are flipped!
Here’s the code for the above little experiment:
void testProj(Point4F testPt) { MatrixF proj(GFX->getProjectionMatrix()); Con::printf(“untranslated: %f %f %f %f”, testPt.x, testPt.y, testPt.z, testPt.w); proj.mul(testPt); Con::printf(“clipspace: %f %f %f %f”, testPt.x, testPt.y, testPt.z, testPt.w); testPt.x /= testPt.w; testPt.y /= testPt.w; testPt.z /= testPt.w; Con::printf(“normalized device coords: %f %f %f”, testPt.x, testPt.y, testPt.z); }
Point4F inFrontOfCamera(-10.0f, 100.0f, 0.0f, 1.0f); Point4F behindOfCamera(-10.0f, -100.0f, 0.0f, 1.0f); Con::printf(“infront”); testProj(inFrontOfCamera); Con::printf(“behind”); testProj(behindOfCamera);